مجموع ریمان:
 |
مجموع مساحت مستطیل های که ما برای تخمین مساحت زیر منحنی استفاده می کنیم. مجموع ریمان نامیده می شود. حال با مثالی این مجموع را توضیح می دهیم:
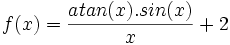 |
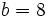 و
و 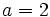
:

با استفاده از مجموع ریمان: 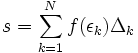
خواهیم داشت:
11.924959 =مقدار دقیق مساحت
11.8740138= مساحت محاسبه شده
بین مجموع ریمان و مقدار دقیق جواب اگر مقایسه ای انجام دهید
در این صورت مقدار خطای با برابر خواهد بود با:
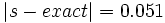 |
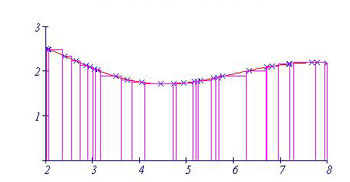
همانطور که مشاهده شد مستطیل ها به صورت رندومی تولید شده اند و تعداد آنها محدود است. حال به نظر شما اگر تعداد مستطیلها یعنی nرا افزایش دهیم و مستطیل ها، حالت منظم به خود بگیرند چه اتفاقی خواهد افتاد.البته توجه کنید که nهای مختلف، مجموع ریمان مختلفی تولید می کنند.
 |
مثال :
می خواهیم مجموع ریمان برای مساحت زیر نمودار منحنی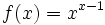 دربازه
دربازه 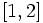 را پیدا کنیم
را پیدا کنیم
1) بازه را به 5 قسمت، از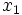 تا
تا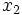 تقسیم می کنیم:
تقسیم می کنیم:
2) عرض مستطیل ها را پیدا می کنیم.
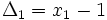
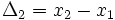
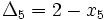
3) نقاط 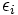 را در بین
را در بین 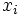 ها برای پیدا کردم ارتفاع مستطیل که برابر با
ها برای پیدا کردم ارتفاع مستطیل که برابر با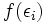 خواهد بود، قرار می دهیم در این صورت:
خواهد بود، قرار می دهیم در این صورت:
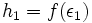
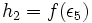
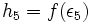
4) پیدا کردن مساحت 5 مستطیل: 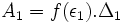 تا
تا 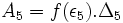 را پیدا میکنیم.
را پیدا میکنیم.
5) مساحت های بدست آمده را با هم جمع می کنیم:
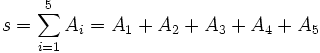 |
انتگرال ریمان:
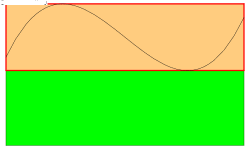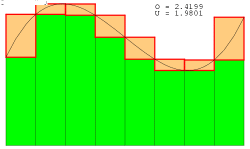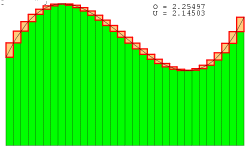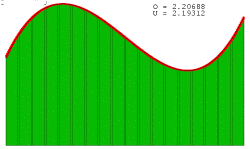 |
را نشان میدهدهر چه قدر بازه ها کوچکتر و تعداد مستطیلها بیشتر میشود مقدار O(حد مجموع بالا)و U (حد مجموع پایین) به مقدار اصلی مساحت نزدیک خواهد شد. |
ممکن است تا اینجا به این نکته رسیده اید که هر چه قدرعددn (یعنی تعداد مستطیلها) بیشتر باشد مجموع ریمان به یک عدد ،همگرا میشود. یعنی حد گرفتن از مجموع ریمان وقتی که n بسیار بزرگ است مساحت زیر نمودار را به ما می دهد.
تعریف انتگرال ریمان:
اگر f تابعی باشد که دربازه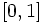 تعریف شده است در این صورت مجموع ریمان تابعf در بازه
تعریف شده است در این صورت مجموع ریمان تابعf در بازه 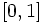 وقتی که n به سمت بی نهایت می رود،همگرا به یک مقدار محدود مانند Aخواهد بود.
وقتی که n به سمت بی نهایت می رود،همگرا به یک مقدار محدود مانند Aخواهد بود.
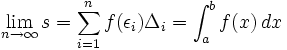 |
 هدف من از ایجاد این وبلاگ ارائه مطالب و نکته های درسی مهم و قرار دادن کتابها و جزوات دانشگاهیه
هدف من از ایجاد این وبلاگ ارائه مطالب و نکته های درسی مهم و قرار دادن کتابها و جزوات دانشگاهیه