دریای ریاضی

منحني مي توانند با بهره گيري از يک خط راست (خط راهنما يا هادي directrix) و يک نقطه (کانون focus) تعريف شوند.

اگر فاصله هاي زير را اندازه گيري کنيد:

الف) از کانون به يک نقطه روي منحني و

ب) خط عمود از خط هادي به آن نقطه؛

خواهيد ديد که نسبت اين دو فاصل هميشه يکسان است؛ به طوري که:

براي يک بيضي نسبت کمتر از يک است.

براي يک سهمي اين نسبت برابر است با يک؛ يعني اين دو فاصله با هم برابرند.

براي يک هذلولي اين نسبت بزرگتر از يک است.

خروج از مرکز (Eccentricity)

نسبت بالا را «خروج از مرکز» مي نامند و بنابراين مي توان گفت که هر مقطع مخروطي (conic section) «تمام نقطه هائي است که فاصله تا کانون برابر است با خروج از مرکز ضرب در فاصله تا خط هادي».

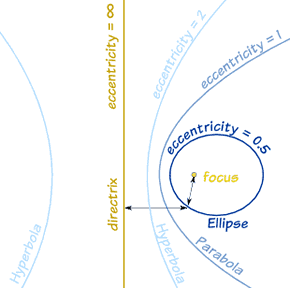
براي 1 > خروج از مرکز > 0 بيضي خواهيم داشت؛

براي خروج از مرکز = 1 سهمي و

براي خروج از مرکز > 1 هذلولي خواهيم داشت.

يک دايره، خروج از مرکز برابر با صفر دارد. بنابراين خروج از مرکز نشان مي دهد که يک منحني تا چه اندازه «نا دايره»اي (un-circular) است؛ خروج از مرکز بزرگتر انحناي کمتر.